Recently, the research team from the School of Physical Science and Engineering at Tongji University has achieved significant progress in the field of topological physics. The team discovered a new class of topological edge states in non-Hermitian gapless systems, fundamentally challenging the traditional bandgap-based theoretical framework of topological protection. The related research findings, titled "Unconventional Topological Edge States in One-Dimensional Non-Hermitian Gapless Systems Stemming From Non-isolated Hypersurface Singularities," have been published in the top-tier physics journal Physical Review Letters (DOI: 10.1103/PhysRevLett.134.206603).
Key Scientific Discoveries
Traditional topological physics theory holds two fundamental premises regarding the understanding of topologically protected edge states: first, topologically protected edge states must exist within the bandgap; second, topological invariants defined based on Berry phase can explain the existence of edge states (i.e., bulk-boundary correspondence), but their definition relies on the existence of a bandgap. Consequently, existing theories consider topological edge states to be inseparable from bandgaps (Fig. 1a-c), leading to the widespread belief in the academic community that band structures without gaps cannot support topological edge states.
Collaborative research by Dr. Hongwei Jia from Tongji University and Dr. Jing Hu from Shanghai University revealed that in non-Hermitian one-dimensional systems with PT symmetry, although exceptional point degeneracies lead to bandgap closure, topological edge states can still exist even when band bands completely overlap (Fig. 1d-f). This important discovery transcends the traditional theoretical framework that "topological protection requires the existence of a bandgap."
Innovative Theoretical System
These non-Hermitian gapless one-dimensional systems originate from swallowtail catastrophe hypersurface singularity degeneracies (Fig. 2a). The Brillouin zone of such systems is obtained by mapping closed loops encircling non-isolated singularities of the swallowtail catastrophe. Due to the non-isolated nature of these singularities, the closed loops inevitably traverse the hypersurface, which is precisely where the exceptional points reside.
To address the failure of traditional topological invariants (such as Berry phase) when bandgaps close due to exceptional point degeneracies, the research team innovatively proposed the "eigenframe rotation and deformation theory." This theory, combined with non-Bloch band theory, successfully explains the physical mechanism of topologically protected edge states in gapless systems. Notably, this theory shows excellent compatibility with the intersection homotopy theory in algebraic topology, which is the fundamental mathematical method for defining topological invariants of non-isolated singularities.
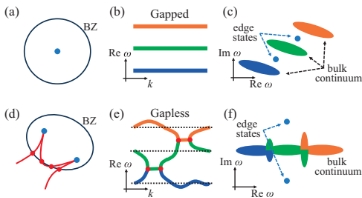
Figure 1
Experimental Verification
Through carefully designed non-reciprocal topological circuits, the research team successfully observed these novel edge states in experiments. The experimental circuits accurately simulated one-dimensional gapless systems constructed based on swallowtail catastrophe singularities, verifying the stability of edge states under band closure conditions (Fig. 2b-d).
Scientific Significance
At the theoretical level, this research extends the concept of topological protection to gapless topological phases, opening new directions for the study of topological phenomena in non-Hermitian systems. In terms of interdisciplinary integration, this work combines catastrophe theory, algebraic topology, and non-Hermitian physics—several cutting-edge fields in physics and mathematics—laying an important foundation for subsequent related research.
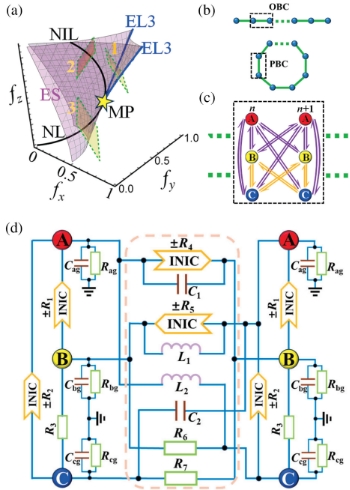
Figure 2
Research Team and Contributions
This research was jointly led by Dr. Hongwei Jia from Tongji University (first author and corresponding author), Dr. Jing Hu from Shanghai University (co-first author and corresponding author), and Professor C.T. Chan from the Hong Kong University of Science and Technology (corresponding author). The collaborating team includes Ruoyang Zhang, Mudi Wang, and Yixin Xiao from the Hong Kong University of Science and Technology; Dongyang Wang from the University of Southampton; Shaojie Ma from Fudan University; Academician Xiaoping Ouyang from Xiangtan University; and Professor Yifei Zhu from the Southern University of Science and Technology, among other experts and scholars.
The paper website:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.206603
